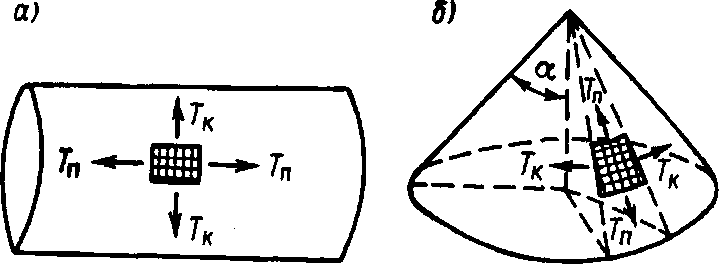
 Рис. 3.2. Натяжения, возникающие в цилиндрической (а) и конической (б) оболочках лодки
в некоторых конструкциях вертикальных перегородок. Натяжения в таких пневмооболочках равны
Здесь се — половина угла при вершине конуса, град; г — радиус сечения, перпендикулярного оси симметрии, см.
Натяжения в вершине конуса равны нулю, на контуре основания — максимальны.
Сферическая оболочка. Сферическую оболочку применяют в основном в тех же конструктивных элементах надувной лодки, что и коническую. Для сферической оболочки натяжения рассчитывают по формуле
где г — радиус сферической поверхности, см. Натяжения в сферической поверхности равны между собой и постоянны по значению по всей ее поверхности.
Тороидальная оболочка. Для упрощения расчетов условно принимают носовую оконечность лодки U-образной формы, а также носовую и кормовую оконечности лодки О-образной формы тороидальными. Поперечное натяжение, возникающее в такой оболочке, определяют по формуле
где г — радиус окружности тора, см. Продольное натяжение на внешней поверхности тороидальной оболочки равно
Т =
* п
pm6r/cos а;
Тк - риз6г/ (2 cos а).
Т„ = Гк =/?из6г/2,
Здесь R — радиус вращения сечения вокруг вертикальной оси (радиус тора), см.
Tn=Pm6r(2R + r)/[2(R + r)], а на внутренней поверхности
Tn=pM36r(2R-r)l[2(R-r)].
|


